How to build a proof tree

This post outlines how to build proof trees visualized in paperproof.

paperproof is a Lean theorem proving interface which feels like pen-and-paper proofs. See more github

It was also presented at the Lean Together 2024 conference: recording.

Overview

I’ll start by describing what is a data structure paperproof expects for visualization. We will call it proof tree. Then I’ll have an overview what information is available from Lean compiler, in particular a data structure which Lean compiler provides called InfoTree.

We will then discuss how you can work with an InfoTree to obtain desirable proof tree representation. Even though we will work through a particular case of paperproof I expect the technique to be generally useful, especially for researchers looking towards scraping more and more “how proof develops” data for AI/ML.

What is a proof tree?

We will use the following proof as an example:

On the picture you see an example of a proof tree rendered with paperproof. Goals are represented as red nodes which form a tree. It comes from the fact that each tactic transforms a goal: either refines, bifurcates or closes it. We will also shortly look at it from a metavariable assignment point of view which will make the tree even more evident. Hypothesis (green nodes) also form a set of trees, but we will not discuss them today.

How a tactic when applied transforms a goal into a set of goals I’d call an Arrow. For example tactic cases h transforms goal 2 into goals [3, 4] where different alternatives of the hypothesis h are assumed. Whether tactic exact Or.inl hq closes goal 4, or in other words transform it into an empty set [].

Note that I’ll consistently mark goals with purple and orange colours, using orange where I want to highlight that goal was formed after tactic application.

What is an InfoTree?

Elaboration in Lean compiler is the process turning Syntax (can be user defined) into something Lean compiler can work with. For example term elaborators will turn Syntax into an Expr (simple dependent-type lambda term). Whether tactic elaborators might assign some metavariables (more on this in a sec) and generate new ones.

Some elaborators just turn Syntax into a simpler Syntax and ask compiler to continue elaboration with other elaborators recursively. To record this delegation an elaborator can wrap the continuation inside withInfoContext with elaboration Info it generated. All Info nodes are organized into the InfoTree. Since Syntax is a tree structure formed by inclusion of syntax ranges the produced InfoTree inherits the same property.

For example in the following proof:

The elaborator for a sequence of tactics Lean.Elab.Tactic.evalTacticSeq was responsible for @ <17,2>-<20,29> syntax range, where <17,2> means line 17 column 2. Taking care of separators and indentation it called elaboration on @ <17,2>-<17,9> and @<18,2>-<20,29> which Lean.Elab.Tactic.evalIntro and Lean.Elab.Tactic.evalCases claimed to take care of.

Of particular interest for us is the TacticInfo info nodes as they capture change of user goals which we draw in the proof tree.

How to extract proof tree arrows from TacticInfo nodes?

Looking at the TacticInfo structure first instinct is to look at the goalsBefore goalsAfter pair and identify it with an arrow in the proof tree. That’s how Alectryon works and first attempt at paperproof parser worked. However, this being enough for the Alectryon proof annotation case, it’s not enough information to connect all goals into a single connected proof tree.

Let’s take a look at some examples:

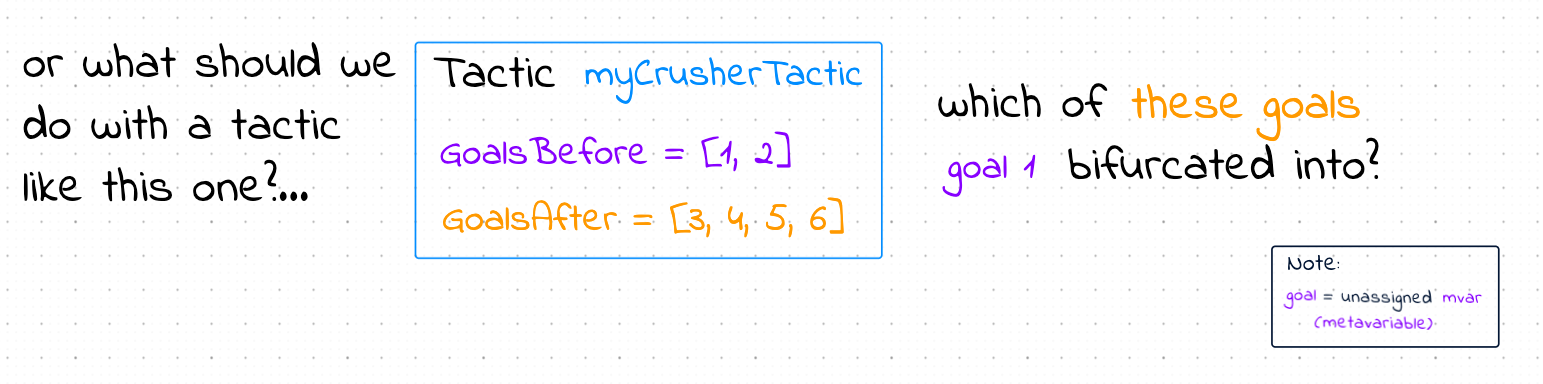
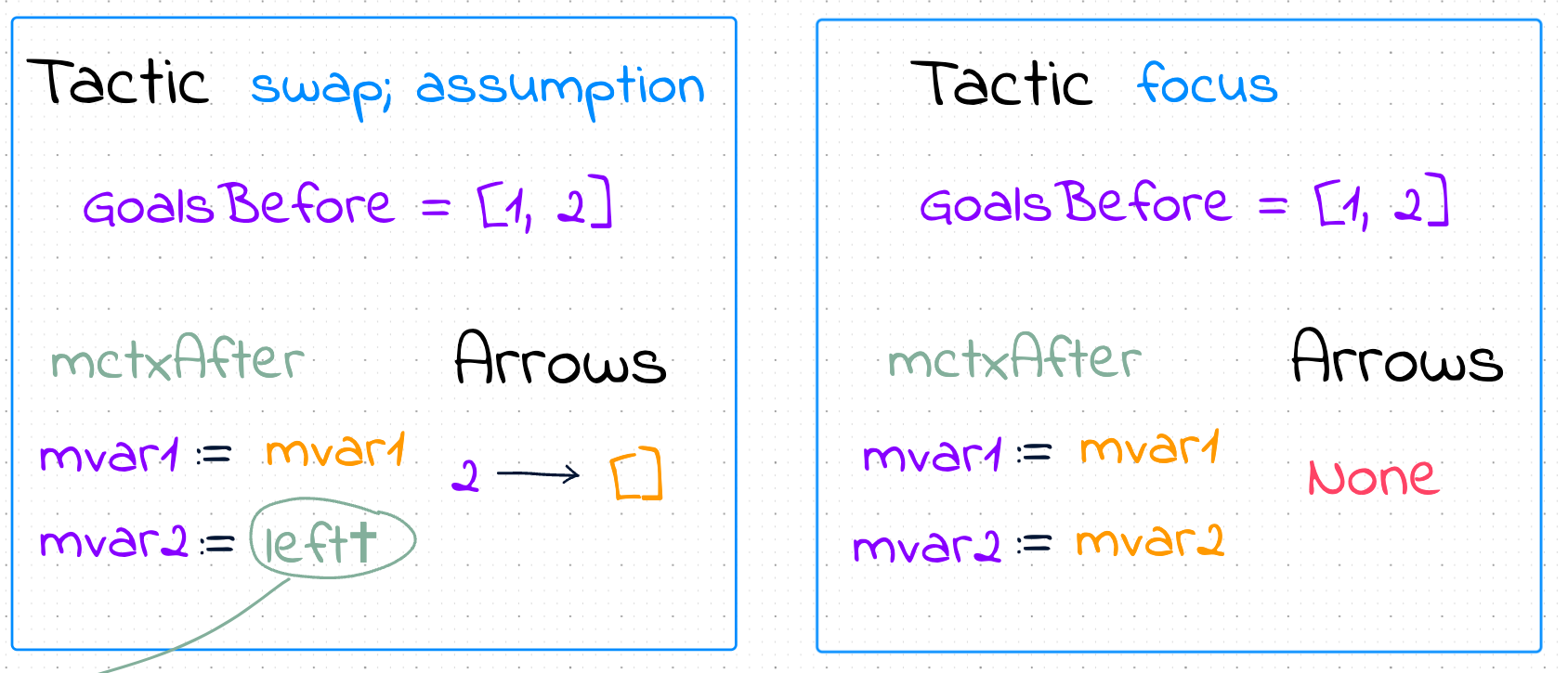
Tactics swap; assumption (swap goals order first and then tries to close first goal by some hypothesis in the scope) and focus (temporarily hides all goals other than the first) have the same goalsBefore/goalsAfter pairs, but should produce different proof trees.

User defined myCrusherTactic somehow simplifies goals (unknown at the time we implement the InfoTree to proof tree parser). In the example above it splits goals 1, 2 into 3, 4, 5, 6, however there is no information, required for the proof tree arrows, on what goals the goal 1 bifurcated into and what goals the goal 2 bifurcated into.

Using MetavarContext to resolve arrows

Other part of the TacticInfo node is how the metavariables context changed. Metavariable is a placeholder for a term that is not yet known during the process of creation of some other term. Metavariable context stores metavariable declarations and their assignments. During it’s execution tactic will assign terms to some metavariables, possibly creating new metavariables as placeholders for parts of these terms.

This gradual clarification of the goal proof term structure through intermediate goals is exactly what proof tree is trying to visualize. We can illustrate it with myCrusherTactic example:

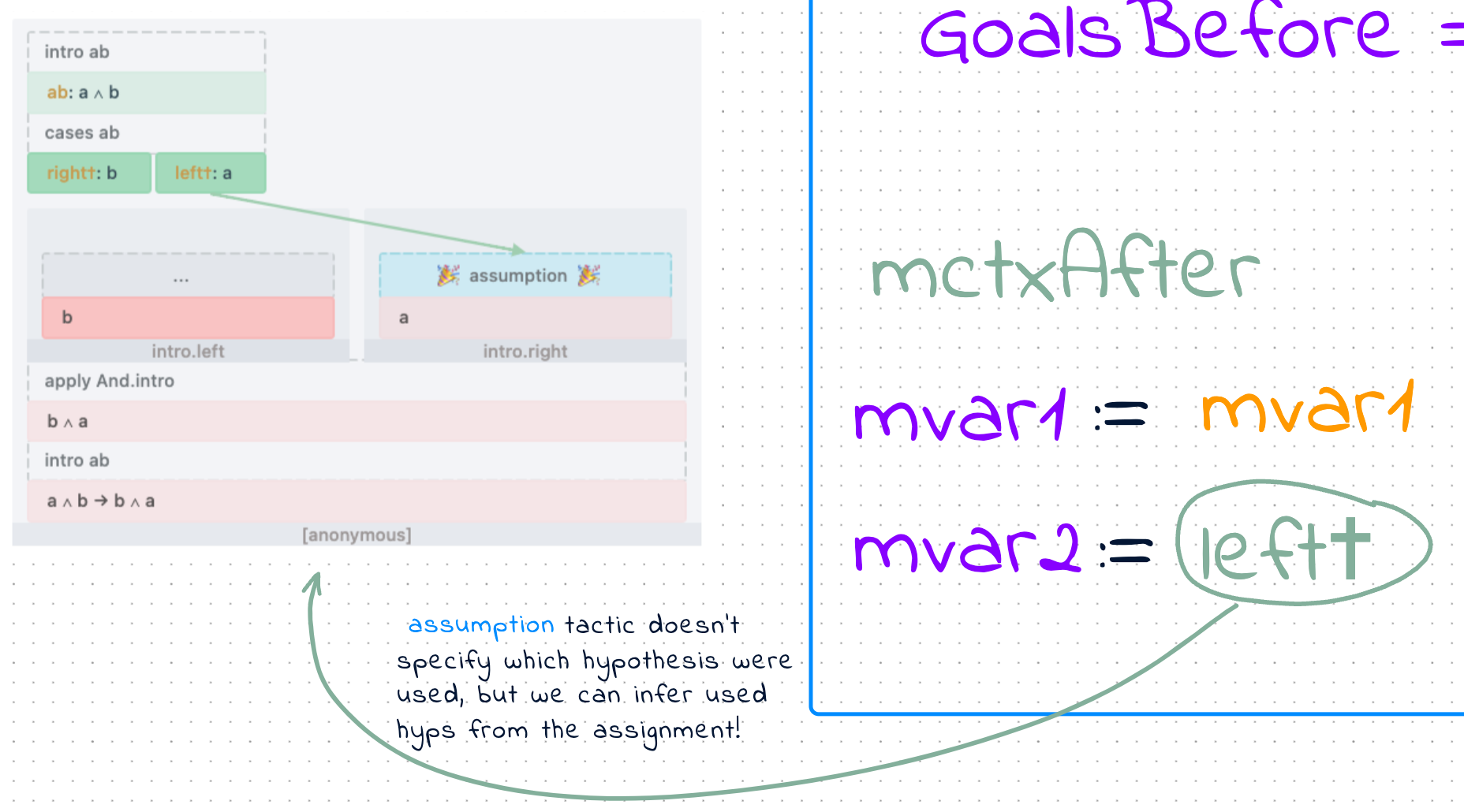
As we see from the term assignment to the goals - myCrusherTactic tries to split all And goals into underlying parts. During this process it introduces new metavariables as placeholders substituting parts of the assigned terms. The correspondence between goalsBefore and newly introduced goals it splits into is easy to establish from the assignment and we can draw arrows in the proof tree accordingly.

Let’s see how we can differentiate swap; assumption and focus looking at the assignments:

As expected focus assigns nothing and therefore generates no arrows, whether swap; assumption finds the term (a hypothesis left-cross) which closes mvar2. Seeing a specific hypothesis in the assignment also allows us to connect assumption tactic with a hypothesis used in the proof tree visualisation:

How to connect all arrows into a single tree

However extracting all arrows information per the algorithm above doesn’t guarantee that we will get a connected tree. The reason for that being that arrows not necessarily have the same granularity.

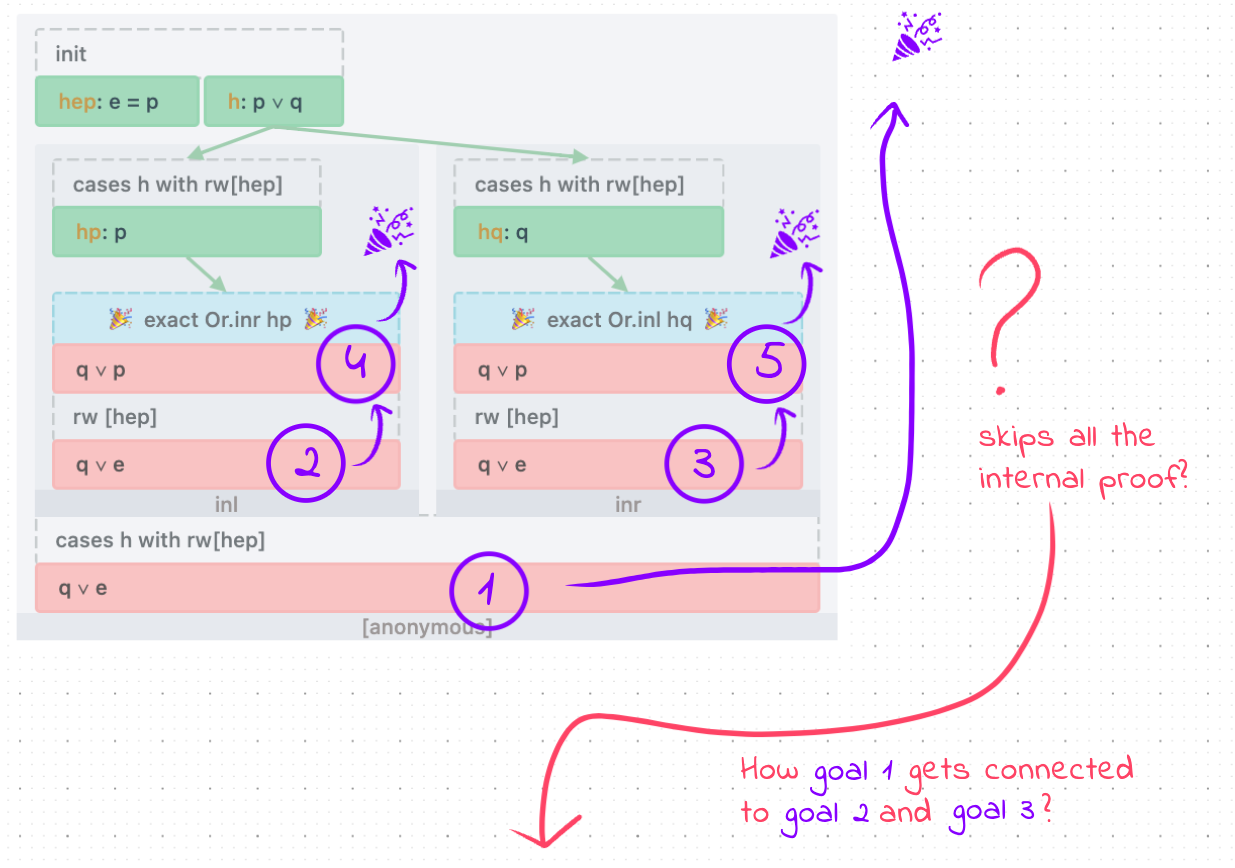
Above you can see the visualisation of the following proof:

From the point of view of the Lean.Elab.Tactic.evalCases elaborator (orchestrating when to call rewrites and how to combine match alternatives) the initial goal is closed after it’s application. However the information other elaborators contributed inside it’s elaboration subtree isn’t connected to the initial goal.

It may seem like we could infer it by looking at the metavarContext, however:

By the time we’re looking at the assignment to mvar1 some mvars which we are interested to establish relationship with might already be instantiated. The only reliable method for us to establish the relationship between user visible goals is by observing how unassigned mvars (aka goals) in mctxBefore connect with unassigned mvars in mctxAfter. However when these probes of the world state are recorded is at the tactic author discretion. The granularity of these probes might vary. We can’t rely that users will push Info node on how the state was prepared before it recursively delegated to other elaborators. To establish the relationship between granularities we will need another trick.

Spawned goals

Relative location of TacticInfo nodes inside InfoTree can be used to infer what tactics were contributing to construction of the proof term for the outer tactic. In the InfoTree subtree for cases tactic we can see all low-level granularity TacticInfo nodes.

How do we establish which TacticInfo nodes goals we should directly connect to the goalBefore of the outer cases tactic? Note that each goal node can’t have more than one incoming goal arrow (otherwise it’s not a tree) and if some goal doesn’t have an incoming arrow (except the top level goal) it wouldn’t be reachable from the top goal. Therefore we conclude that a reasonable choice is to connect goalBefore to all InfoTree subgoals with no incoming arrows. We would call these goals justifying goalsBefore/goalsAfter transition the spawned goals and will depict it in a second square brackets in our arrow notation: 1 -> [], [2, 3].

How tactics like have fit into the model?

To wrap up let’s take a look how tactics like have fit into the model and can be handled in generic way instead of a hardcoded handling of have tactic. The example above generates the following arrow for the have tactic: 1 -> [2], [3, 4]. You might have thought that the goal doesn’t change during have, but even though the type doesn’t change and we still need to prove 3 < 5 the hypothesis in the context are extended with h1: 3 < 4 and h2: 4 < 5. You can think of it as generating the following assignment mvar1 := let h1 := ... in let h2 := ... in mvar2.

However in the final proof tree rendered by paperproof you wouldn’t see a new node for the goal 2 and the goal 1 node will be reused. This UI decluttering is possible when the goal doesn’t bifurcate (we don’t need a new scope box) and keeps it’s type unchanged (no new red node needed either). One other implication is that spawned goals can be lifted up and displayed directly above the hypothesis introduced instead of bifurcating the final goal. Note that the decluttering condition doesn’t check if it’s a have tactic anywhere, it’s capable to draw conclusion simply looking at the arrow information.